La diminution de l’obliquité de la Terre

Partie 1
Le nouveau résultat

Il y a deux ans, en 2016, mon livre “La Croix de l’Année solaire: Sauts dans la chronologie historique” est apparu en allemand (voir l’article go http://www.ilya.it/chrono/frpages/jahrkreuz.html.
Il y avait des réponses favorables et encourageantes, mais pas de critique sévère, comme si seulement des choses bien connues ou évidentes avaient été exprimées dans ce livre.
Bien entendu, certaines choses doivent être réexaminées, réfléchies ou discutées. Les “sauts de précession” sur lesquels le livre se concentre plus que dans les livres précédents, doivent être compris avant d’être acceptés.
Sur un point important, je me suis écarté de toutes les opinions précédentes: je rejette la thèse commune que dit que l’obliquité de l’orbite terrestre se réduit drastiquement quand des sauts de pôle se produisent.
L’obliquité de la terre sur son orbite, l’angle epsilon (ε), diminue constamment. Mais si ce «mouvement est uniforme sur une longue période, on ne peut que le deviner», dis-je p. 126. En tout cas, je rejette les spéculations audacieuses de tous les prédécesseurs que cet angle change radicalement à cause d’une “secousse des pôles”. Anciennement on se référait au modèle mythologique (auteurs comme Anaxágoras et même Hérodote): Dans les temps anciens l’axe de la Terre était perpendiculaire à son orbite, alors il n’y avait pas de saisons, le printemps éternel régnait sous nos latitudes. Je l’ai répété en 1977 (“L’héritage des Géants”). Maintenant, dans le chapitre “opposition” (2016, p 266), j’ai clairement indiqué que je considère cette idée fausse en ce qui concerne les derniers changements de pôles, et cela va à l’encontre de l’opinion de tous les catastrophistes des siècles passés ou d’aujourd’hui.
Christoph Marx toute sa vie supportait cette théorie tenue par les catastrophistes: qu’avant le saut l’angle epsilon était de 32°, contre environ 23° 30′ après le saut (comme maintenant). Il a conclu ceci de la durée de la «grande année» de la précession qui était de 36.000 ans pour Hipparque, et maintenant elle est fixée à 25.900 ans.
La conclusion est fausse, comme je dis dans mon livre (2016, p.268):
« Au temps de Ptolémée l’obliquité était de 23,9° (ou 24°). Si nous transférons les données sur le cercle complet de Ptolémée de 36.000 ans, alors il n’y a qu’une seule conclusion: L’orbite annuelle de la Terre (ou dans la vision ancienne: du soleil) doit avoir duré environ cinq minutes moins, et c’était exactement la valeur qu’Hipparque avait calculée à partir du mouvement du jour de printemps dans le calendrier (365 ¼ jours). Il bouge un jour dans 300 ans, Ptolémée avait confirmé. »
L’hypothèse de grands sauts de l’obliquité de l’écliptique au cours des temps historiques est donc erronée. Pour vérifier cela, j’examinai les astronomes écrivains arabes comme Battani, qui avait mesuré l’année tropicale avec deux minutes de moins, alors que l’obliquité a continué de baisser légèrement dans son temps. Par conséquent, il n’y a pas de dépendance directe entre les deux valeurs (durée de l’année et epsilon).
Conclusion: « Le saut de précession défini par nous ne conduit pas à un grand changement soudain dans l’obliquité, mais au plus un léger redressement de la terre pour quelques minutes d’arc. Généralement, epsilon a peu changé au fil des siècles, indépendamment des changements dans la précession. » (2016, p.288).
Cette conclusion est fondée sur des valeurs traditionnelles astronomiques et est conforme à la situation actuelle (je me réfère au manuel de Julius Dick). Dans la « La Croix de l’Année solaire », je souligne ce résultat à plusieurs reprises, et enfin, dans le chapitre « projet » (2016, p 444), une fois de plus.

Dans la description du modèle des sauts de précession (2016, p.147), je dis expressément:
“La position que forme l’axe de la Terre avec son orbite, l’angle de l’écliptique, ne change pas essentielleemt – sauf quelques fluctuations minimales qui doivent être supposées …”
La durée de l’année tropicale a parfois brusquement diminué considérablement tandis qu’epsilon n’a pas été affecté, mais a souffert approximativement du même degré de réduction usuel.
Maintenant, je voudrais expliquer cette découverte un peu plus largement, car l’erreur suivante poursuit encore les méthodes de datation des archéo-astronomes:
Parce que « dans les 6000 dernières années » (Wikipédia) la diminution de l’obliquité de l’écliptique est sans interruption, il est assez simple de déterminer l’âge d’un bâtiment ou d’un texte astronomique si’l contient une indication de l’angle précis d’epsilon (ε) directement ou caché: L’équation de la variation d’epsilon actuelle est appliquée et avec elle on obtient la différence de temps qui s’est écoulée jusqu’à présent.

Partie 2
Le problème de la mesure, considéré par l’exemple de la latitude géographique dans l’Antiquité

Lorsqu’on considère les valeurs classiques de la latitude nord de nombreuses villes dans le monde habité (l’Oekoumène), mentionnées par Ptolémée (Geografike « 140 après JC. ») et ses prédécesseurs, en particulier Strabon et Pline, et aussi Hipparque, il est à noter que les données sont de fiabilités variables. La grande majorité des valeurs a été calculée, et non mediée sur place à l’aide du soleil ou les étoiles, mais a été calculé en fonction de la longueur du jour du solstice d’été par rapport à la nuit, et ça (pour la simplicité) à l’echelle d’ intervalle de quart d’heure, donnant comme résultat des valeurs arrondies. Dans Ptolémée (Syntaxe), les valeurs de latitude apparaissent à intervalle de 5 minutes d’arc.

Les rares données observées (voir note 1) sont en bon accord, mais toutes sont supérieures de 10 à 20 minutes d’arc. Il est conclu (Peschel 1877, p.43) que cela a été généré à cause d’une erreur systématique en se référant au bord supérieur de l’ombre du gnomon, pas au centre du soleil, ce qui rend le résultat plus grand jusqu’à 16 minutes d’arc (voir Fig. 1). La réfraction atmosphérique peut renforcer ce résultat par une minute d’arc seulement, parce que l’angle est mesuré lorsque le soleil est à son point le plus haut, tandis que lorsqu’il est à l’horizon, l’augmentation serait considérable en fonction de l’humidité ambiante.

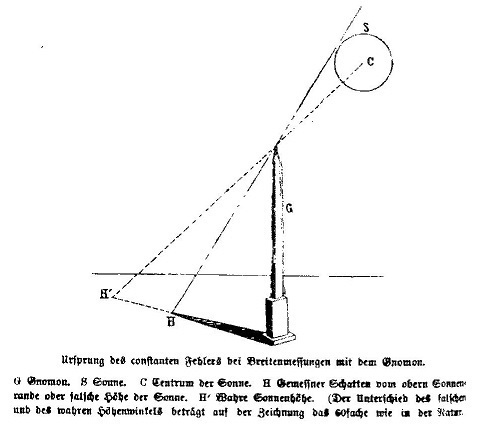
Fig. 1: Arpentage de latitude avec le Gnomon (selon Peschel p. 44)

Contre l’accusation d’une erreur systématique de lecture causée par les astronomes de l’Antiquité, qui est reconnue par tous les érudits actuels de l’histoire de l’astronomie, je soulève une objection: ils ont intentionnellement mis un globe sur l’obélisque (le gnomon ) et ensuite surmonté par une petite croix ou un pique pour que l’erreur de lecture puisse être évitée. Un regard à travers un trou dans la pierre évite la même erreur. Les deux artifices sont connus depuis l’Antiquité.
Les valeurs “trop ​​élevés” pour epsilon par les géographes anciens pourraient être justifiées.
Au moins, cette affirmation reste juste: Ératosthènes a mesuré un plus grand angle d’epsilon quand, par les extrapolations actuelles, il doit avoir mesuré moins: il a mesuré 23° 51′ 20″. Pourquoi?
Pour répondre à cette question, il existe trois modes (voir aussi note 2):
1) pourquoi Ératosthène était-il incapable?
2) Ératosthène ne pouvait pas avoir tort;
a) parce que l’intervalle de temps était plus long que les indications historiques, ou
b) que les projections actuelles de l’algorithme d’epsilon doivent être fausses.

On parle du déplacement de l’axe de la Terre, la réduction d’epsilon, l’inclinaison de l’équateur terrestre par rapport à son orbite. Cette diminution d’epsilon est calculée au moyen d’une formule moderne en relation au temps, ce qui indique que les valeurs mesurées par les astronomes antiques sont trop élevées.
Si elles allaient être justes? Ensuite, la diminution d’epsilon dans le passé serait arrivé plus rapidement que nous supposons aujourd’hui.
Il y a déja quelques années, cette réponse me semblait être la meilleure explication; cela n’a pas d’importance pour les sauts de précession projetés par moi, comme j’ai souligné en 2016: la tendance du changement de l’axe terrestre est trop faible pour impliquer des défauts notables des dates.
En revanche, il est à souligner: les valeurs de datations astronomiques des monuments mégalithiques produits par les archéologues, qui sont plus élevés que d’habitude par des millénaires, semblent peu fiables en raison de l’inexactitude de ce calcul. Au moins, il faut prendre en considération ce que Peschel a observé à cet égard.

Partie 3
Résultat

L’algorithme de calcul de datation actuelle indique que la variation de l’écliptique est cyclique sur une période d’environ 40.000 ans qui reviendra à une valeur similaire dans les 40. 000 ans. La courbe parabolique descendante ou ascendante prend environ 20.000 ans. Dans un graphique (selon Laskar 1986, voire note 3), reflétant le résultat de l’extrapolation des données de mesure actuelles et de l’influence calculée des planètes sur la base de la théorie de la relativité, on peut facilement juger que l’obliquité réduit constamment au cours des 8.000 dernières années, et qui augmente auparavant. Vers 6.000 avant JC, epsilon était de 24° 12′. Le point le plus élevé a été atteint vers 3.000 avant JC. avec 24°. Comme la courbe ne change pas brusquement mais de façon plutôt sinusoïdale, l’augmentation et la diminution de ses points d’inflexion sont très graduelles. Nous sommes maintenant au milieu de la courbe descendante, qui est presque rectiligne, de 4.000 avant aujourd’hui (BP) à 3.000 après aujourd’hui. Il continuera à diminuer pendant quelques milliers d’années, jusqu’à 22° 30′, puis augmentera progressivement.

Par hypothèse classique, Ératosthène a prospéré autour de 2.200 avant aujourd’hui. Selon l’ équation moderne, il devait mesurer pour epsilon un valeur autour de 23° 43′, soit environ 8′ de moins que la mesure qu’il avait obtenue (23° 51′ 20″). S’il y avait une lacune dans le temps historique (notre théorie), sa date nous approche: en réduisant un millénaire, Ératosthènes devait mesurer 23° 36′, soit 15′ de moins (un quart de degré).

Vraisemblablement, les sauts de précession auront causé de très petits changements par epsilon, mais attention: petits. Les saisons auront changé en réduisant l’écliptique pendant quelques minutes d’arc, étant donné que la différence entre 24° 5′ (note 4) et 23° 50′ importent 15 minutes d’arc, qui correspond à la différence calculée actuellement entre aujourd’hui et l’Empire romain. Des sauts de précession et des phénomènes similaires sur d’autres planètes qui influencent epsilon peuvent expliquer les résultats de mesures d’Ératosthène. La nature saute, et l’écliptique également dans une très petite mesure, pas significatif pour nous.
La question était: les extrapolations de la situation actuelle sont-elles fausses, car elles nécessitent une régularité excessive des mouvements de la Terre (et du système solaire en général)? ou sont-ils invalides parce que le moment historique n’a pas été évaluée correctement, de sorte que les dates projetées sont correctes dans une autre échelle chronologique?
Pour transférer Ératosthène conformément aux valeurs extrapolées, il aurait dû vivre antérieurement, beaucoup plus longtemps qu’accepté. Une réduction du passé (notre thèse) aboutirait à ce que le moment attribué à Eratosthène soit projeté dans un passé très lointain. Cela changerait définitivement notre vision de l’histoire.
Si nous ne l’acceptons pas, la faute n’est pas l’échelle du temps historique (la chronologie traditionnelle), mais l’adoption d’un mouvement continu des corps célestes. Même dans la vie de Copernic (c’est-à-dire 500 BP), la graphique de Laskar dévie légèrement (elle est plus raide). Copernic médiait epsilon de 23° 28′, alors que le schéma Laskar obtien 23° 30′ 20″ indiquant 2′ plus. Laskar n’est pas perturbé par les documents historiques, alors que je suive Copernic (2016, p. 205). Qui ne prend pas en compte les changements chaotiques historiquement connus (sauts, etc.) et observés dans le cosmos, poursuit une image purement théorique du passé, sans aucune prétention de la réalité.

Bibliographie

Dick, Julius (1965): Grundtatsachen der sphärischen Astronomie (Leipzig)
Mžik, Hans von (1938): Theorie und Grundlagen der darstellenden Erdkunde (Geografike des Ptolemaios) avec collaboration de Friedrich Hopfner (Gerold, Vienne)
Peschel, O. (1877): Geschichte der Erdkunde, 2.ed. (München)
Ptolemée, Sintaxis – Manitius, Karl (1912-13): Des Claudius Ptolemäus Handbuch der Astronomie (Teubner, Leipzig, 2 vol., trad. du grecque a l’alemande, reprint 1963)
Vitruv (1908): Diez livres sur l’arquitecture, trad. alemande par Dr. Franz Reber (Berlin; Wiesbaden 2004)

Notes

1)
Peschel 1877, p. 45:
Ératosthènes (dans Strabon) mentionne pour Alexandrie 30° 58′ (au lieu de: 31° 11′) – 13′ plus haut
Hipparque a pour Rodos 60: 43 5/6 = 36° 8′ 7 “(au lieu de 36° 25′) – 17′ plus haut
Pitheas donne pour Marsilia 42° 57′ (au lieu de 43° 17′ 47″) – 20′ plus haut
pour Canopus il est donné: 31° 5′ (au lieu de 31° 19′ 14″) – 14′ plus haut
Peschel veut montrer que les anciennes valeurs sont toujours inférieures d’environ 16′, parce que seul le bord supérieur du soleil a été utilisé, c’est-à-dire que le centre du soleil au solstice d’été est plus bas qu’indiqué par le bord supérieur de l’ombre (il apporte un dessin p. 44, ici fig. 1)

Vitruv, De architectura IX:
Rome 8: 9 = 0,888 = 41° 35′ – le valeur éxacte serait 41° 53′ 30″ (18′ plus haut)
Athène 3: 4 = 0,75 = 36° 55′ – éxacte: 37° 59′ (64′ plus haut)
Rhodos 5: 7 = 0.714 = 35° 32′ – éxacte 36° 11′ (39′ plus haut)
Tarent 9: 11 = 0,82 = 39° 20′ – éxacte 40° 24′ (64′ plus haut)
Alexandrie 3: 5 = 0,6 = 31° – éxacte 31° 12′ 20″(12′ 20″ plus haut)
Parce que les fractions doivent être formulées par de petits unitées entieres et géométriquement exprimables, les résultats sont assez bons. Toutes les valeurs modernes sont donc plus élevées (deux même plus de 1°).
Si la latitude phi (ɸ) est trop faible, epsilon (ε) a été plus élevé.

2) Il y a aussi d’autres réponses possibles: par exemple, la référence à la dérive des continents; ou un réel changement du pôle (que je rejette pour la courte période considérée ici), ou des erreurs de calcul rectifiées aléatoirement (ça aussi!).

3) réf. Laskar (selon Wikipédia anglais):
< Au cours des 5 derniers millions d’années, l’obliquité de la Terre a varié entre 22° 2′ 33″ et 24° 30′ 16″, avec une période moyenne de 41.040 ans. Ce cycle est une combinaison de précession et le plus grand terme dans le mouvement de l’écliptique. Au cours du prochain million d’années, le cycle portera l’obliquité entre 22° 13′ 44″ et 24° 20′ 50”.
< La Lune a un effet stabilisateur sur l’obliquité de la Terre. L’analyse des dates de fréquences faite en 1993 suggère qu’en l’absence de la Lune, l’obliquité peut changer rapidement en raison des résonances orbitales et du comportement chaotique du système solaire, atteignant 90° en seulement quelques millions d’années.

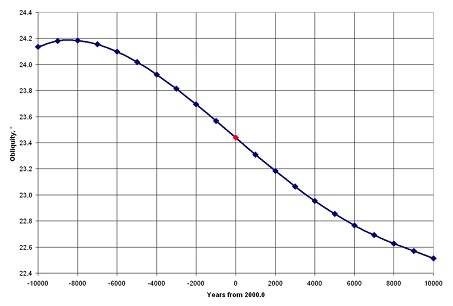
Fig. 2: Laskar 1986

4) La valeur de l’angle d’obliquité (ε) à l’époque d’Ératosthène, comme il était censé l’avoir calculé, était la moitié de 11/83 du cercle complet, c’est-à-dire 23° 51′ 20″. Le tropique du Cancer (dans le lieu de Syene, aujourd’hui Asuan), utilisé pour son calcul de la taille de la terre, était un peu plus de 24°, exactement 24° 5′ (= 24 1/12). La deuxième déclaration probablement n’est pas été mesuré par Ératosthène lui-même, mais venait d’une antiquité lointaine.
Wikipédia poursuit: < Déjà au Ve siècle av. J.-C., Oynopides avait donné l’altitude de Chios à 24° >. Je comprends cela, parce qu’il vivait antérieur à Ératosthène, donc epsilon était plus proche de 24°.

Uwe Topper avec la cooperation de Ilya Topper, Avril 2018